I think I found two errors in the book here, They are highlighted in red below.
Part 1 Causality jargon
This section was introducing a ton of jargon and, as ever, Carroll confused me with his brevity and power sentences. Early on we had an
achronal hypersurface which is one where no two points are connected by a timelike curve. Carroll gives any edgeless spacelike hypersurface in Minkowski space as an example. I was having a bit of trouble imagining an 'edgeless spacelike hypersurface in Minkowski space' when I found Fig 1. That made it obvious. The HYPERSURFACE OF THE PRESENT therein is achronal.
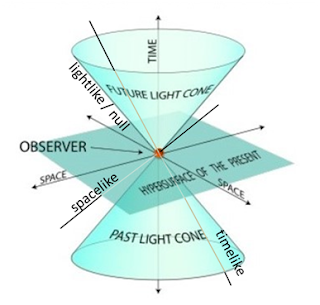 |
| Fig 1 |
I was confused by the long noun phrase 'edgeless spacelike hypersurface in Minkowski space'. Thank heavens it was not in German, it might have been Minkowskistumpfraumsechthyperfläche. As a reminder we classify the following straight lines through the observer:
timelike
|
inside the light cone - massive
particle
|
null (aka lightlike)
|
on the light cone - photon
|
spacelike
|
outside the light cone
|
On a flat
(x,t) spacetime diagram any line is a hypersuface, if it's edgeless it continues forever and it is spacelike if its gradient
m is always limited: -1 <
m < 1 - it is more parallel to the space axis than the time axis.
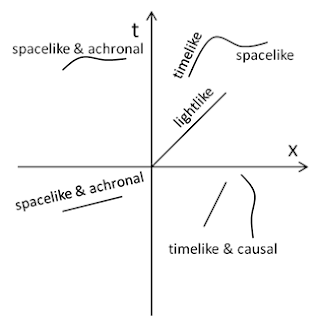 |
| Fig 2 Various types of hypersurface. Both spacelike surfaces are achronal. |
The upper right 'hypersurface' is timelike, null and spacelike because it is steep at the left hand end and then shallow. The spacelike hypersurfaces are also achronal, they do not contain any points that are connected by a timelike curve.
Thinking about an achronal hypersurface S, Carroll defines one + four (or eight) new terms.
Causal curve
|
|
One which is timelike or null
everywhere. Two are shown.
|
Causal future of S
|
J+(S)
|
Set of points that can be
reached from S by following a future directed causal curve
|
Chronological future of S
|
I+(S)
|
Set of points that can be
reached from S by following a future directed timelike curve
|
Future domain of dependence of
S
|
D+(S)
|
Set of all points that p such
that every past moving inextendible* causal curve through p intersects S.
Points predictable from S (see below).
|
Future Cauchy horizon of S
|
H+(S)
|
Boundary of D+(S).
Limit of predictable points (see below).
|
The other four definitions follow by exchanging past and future and + and -.
* inextendible means the curve goes on forever.
We'll now concentrate on the spacelike hypersurfaces S and T, which are achronal, in fig 3.
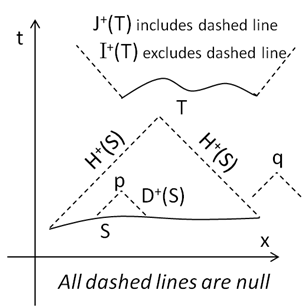 |
| Fig 3 |
The futures of T are easy to visualise. It is also easy to see that p is in D+(S) and that q is not, so D+(S) is the interior of the 'triangle' with the wavy bottom bounded by two null surfaces.
Before all the definitions, Carroll had mysteriously said that "We look at the problem of evolving matter fields …".
Light dawned: The evolution from events (the initial conditions) in S can only completely specify future events in D+(S) its future domain of dependence. Events beyond its future Cauchy horizon cannot be predicted from the initial conditions.
There were some more terms
Cauchy surface
|
Closed achronal surface Σ whose
domain of dependence D+(Σ) is the entire manifold
|
Globally hyperbolic
|
A space time that has a Cauchy
surface
|
Partial Cauchy surface
|
? Cauchy surface whose domain
of dependence D+(Σ) is not the entire manifold
|
Closed time like curve
|
See below
|
From information on a Cauchy surface on we can predict what happens throughout the entire manifold / entire universe / all spacetime.
Part 2. Cylindrical spacetime
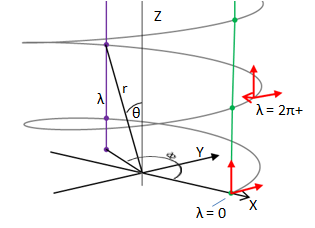
We then have a simple example: Consider a two-dimensional geometry with coordinates ##\{t , x\}##, such that points with coordinates ##(t , x)## and ##(t , x+1)## are identified. The topology is thus ##\boldsymbol{\mathrm{R}}\times S^1##. We take the metric to be
$${ds}^2=-{\mathrm{cos} \left(\lambda \right)\ }{\mathrm{d}t}^2-{\mathrm{sin} \left(\lambda \right)\ }\left[\mathrm{d}t\mathrm{d}x+\mathrm{d}x\mathrm{d}t\right]+{\mathrm{cos} \left(\lambda \right)\ }{\mathrm{d}x}^2$$where$$\lambda ={{\mathrm{cot}}^{-1} t\ }$$which goes from ##\lambda =0## (##t = - \infty ##) to ##\lambda = \pi## (##t = \infty ##).
##\lambda ={{\mathrm{cot}}^{-1} t\ }## is the same as ##\lambda ={\mathrm{tan}}^{-1} ( 1 / t )## and so
$$t=\ 1 /{\mathrm{tan} \lambda \ }$$
That's a problem. As ##\lambda \to 0, t \to \infty ## not ##-\infty ##. So we really want
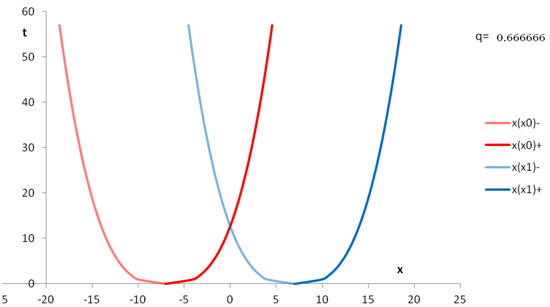
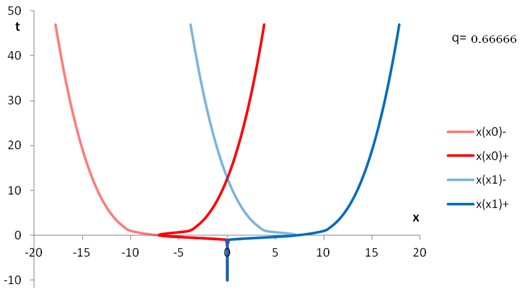
$$\lambda =-{{\mathrm{cot}}^{-1} t\ }$$To find the light cone we want a null vector ##V^{\mu }##, at various times. We can get this from the metric and Desmos plotted various light cones from 0 to ##\pi## as shown below. Details are in the pdf. I had arrived at the same diagram as Carroll!
Fig. 4. Shows the light cones in red in the distant past (λ = 0) to distant future (λ = π). In our diagram we are identifying points with coordinates (t,x) and (t, x+~100), so that we can better see the strange light cones for large t or λ≈π .
Our light cones rotate the same way as Carroll's Fig 2.25.
Carroll says "When t > 0, x becomes the timelike coordinate." (Because x, not t, is in the light cone. Moreover light and particles can only move in the positive x direction and they can move in + and - t directions.) We can now draw two causal curves from a point p as shown. One reaches the surface S, the other does not. Therefore p is outside the future Cauchy horizon of S. This applies to any point p with t > 0. As he says "There is thus necessarily a Cauchy horizon at t=0." Surely it's worse than that. There is a 'global' Cauchy horizon at t = 0. Perhaps that is what he meant.
In plainer language: "Nothing at t > 0 is predictable by things at t < 0".
I don't see why we had to have the cylindrical coordinate system. The closed causal curve guarantees that the causal curve from p is inextendible, but we could have had a curve that waved around forever keeping its t coordinate always >0.
Part 3 A singularity
There seems to be another error in the book here. His fig 2.26 shows a singularity at a point p and the text discusses a point p that is in the future of the singularity. So I will repeat the paragraph and the diagram using separate p's.
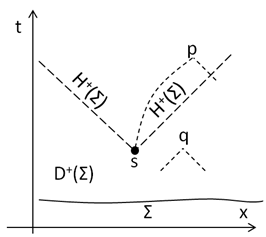 |
| Fig 5 |
It starts clearly enough, "Singularities are points that are not in the manifold even though they can be reached by travelling along a geodesic for a finite distance. Typically they occur when the curvature becomes infinite at some point; if this happens, the point can no longer said to be part of space time." Now I take over.
Fig 5 shows a singularity at s and an achronal surface Σ that extends indefinitely in the plus and minus x directions. The point p cannot be in D+(Σ), future domain of dependence of Σ, because there are causal curves from p that end at s. Therefore there is a future Cauchy horizon at H+(Σ) as shown. H+(Σ) also extends indefinitely in the plus and minus x directions.
I am not sure if the right branch of the past light cone from p should escape the influence of the singularity, but it does not matter for this argument.
Part 4. A Diversion
From fig 4 it is clear that photons and particles from t > 0 can travel backward in time to t = 0 or nearby. Sadly I was not able to find the equations of motion. I need to know more about geodesics perhaps.