Pythagoras's and Newton's formulas for 𝝅

This fun video by Veritasium gives the story of Pythagoras and Newton and ##\pi## but it doesn't go into details. I wanted to know more.

Pythagoras calculated ##\pi## by placing regular n-agons just inside and outside a unit circle and calculating their perimeters. Some examples are shown below.

Apparently he stopped at a 96-agon. I reckon the result he got was$$48\sqrt{2-2\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{4}\sqrt{2+\sqrt3}}}}<\pi<\frac{96\sqrt{2-2\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{4}\sqrt{2+\sqrt3}}}}}{\sqrt{2+2\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{4}\sqrt{2+\sqrt3}}}}}$$It was accurate to four significant digits and not surprisingly he stopped! He didn't even have decimal numbers.

The second last person to use this method in anger was Ludolph van Ceulen in about 1600 who did a ##2^{62}##-agon and still only got 35 decimal places. Apparently it took him 25 years. Nutter.

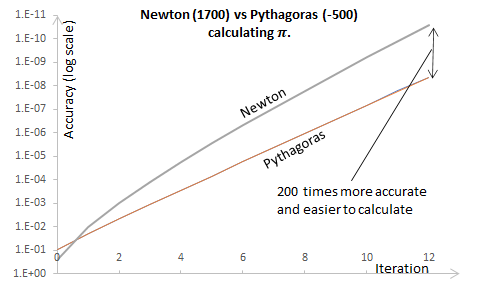
Then along came Newton (about 1700) and he used calculus (which he had just invented) and the binomial theorem to get$$\pi\approx-\frac{3\sqrt3}{2}+6-\left(\frac{1}{4}+\frac{3}{320}+\frac{45}{53,760}+\frac{1,575}{22,855,680}\right)$$That's accurate to five significant digits and a good deal easier to calculate. The further you go the better it gets:

Here's how they did it Newtons formula for pi.pdf (10 pages).

Kinetic Energy ≠ ½mv²

While studying ##E=mc^2## I keep noticing that kinetic energy is not ##\frac{1}{2}mv^2## as we were always taught in school. The relativistic formula is, in various forms, $$K_{rel}=\frac{c^3}{\sqrt{c^2-v^2}}-c^2=c^2\left(\frac{1}{\sqrt{1-\beta^2}}-1\right)=c^2\left(\frac{1}{2}\beta^2+\frac{3}{8}\beta^4+\ldots\right)$$where ##\beta=v/c##.

On May 2nd 2021 the Parker Solar Probe achieved a velocity of 532,000 km/h which is about ##0.0005c##. That gives

\begin{align}\frac{K_{rel}}{c^2}=1.25000023\times{10}^{-7}\ ,\ \frac{K_{cl}}{c^2}=1.25\times{10}^{-7}&\phantom {10000}(8)\nonumber\end{align}Not much difference. The mass of the probe is about 600kg so the difference is ##2.3\times{10}^3\ Joules## which might keep a phone going for an hour.

 

The difference is more noticeable at much higher velocities. At ##0.1c## the difference is about 1%. It goes wild as you approach the speed of light.

A bit more here: 2.2 Kinetic energy.pdf (1 page)

Why does E=mc²?

Trying to follow the second worked example in Box 2.2 of Misner, Thorne, Wheeler I realised that I did not know how Einstein proved ##E=mc^2## and, when I checked in my books, both MWT and Carroll gloss it over! Using Einstein's 1905 paper, an internet video and the relativistic Doppler shift formulas given by Wikipedia I now do. Here's my version based on those.

We take two scenarios 

1) observe the object, in its rest frame, emitting two pulses of light with energy ##E/2## in opposite directions so that it does not change velocity and then we take off in a rocket with velocity ##v## so the object has some kinetic energy ##K_1## 

2) measure its kinetic energy ##K_2## from a frame moving with velocity ##v## then it emits the light which will have energy doppler shifted according to $$E_r=E\left(1+\frac{v^2}{2c^2}\right)$$After the emission we are now in the final state of scenario 1 and the object must have kinetic energy ##K_1## and total energy ##K_1-E##.

In both scenarios the object lost energy by radiation and gained kinetic energy (because the observer started moving) and we end up at the same place. The total energy must be the same in either scenario therefore$$K_1-E=K_2-E\left(1+\frac{v^2}{2c^2}\right)\Rightarrow\frac{Ev^2}{2c^2}=K_2-K_1$$We know how to calculate the kinetic energy (##mv^2/2##) and the velocities of the kinetic energies are the same so the masses must have changed. So$$\frac{Ev^2}{2c^2}=m_2\frac{v^2}{2}-m_1\frac{v^2}{2}\Rightarrow E=\Delta Mc^2$$where ##\Delta M## is the change in the mass of the object. Furthermore we conclude that if one could get all the energy out of an object of mass ##m## that energy would be

$$E=mc^2$$For more details including the derivation of ##E_r## see the very short 2.2 Box E=mc2.pdf.

Coming soon. More on that Box 2.2.

2.5 Differential forms

Vector ##U## (solid) and
1-form ##\widetilde{U}## (dashed)

In section 2.5 of Misner, Thorne, Wheeler 'differential forms' or '1-forms' are introduced and there is soon a fairly elaborate recipe for constructing 1-forms ##\widetilde{U}## from a vector ##U##. I reproduce it below. I tried out the recipe on some of the sample vectors shown and it seemed to work. A one form ##\widetilde{U}## is shown as a set of planes, whose spacing is defined, and which have a positive sense, or direction, as shown by a dashed arrow (which is not a vector). It would seem that you could equally well show the 1-form by a dashed arrow perpendicular (in the Euclidean sense) to the planes whose direction and length would show the positive sense and the spacing of the planes of ##\widetilde{U}##. You can. And I implemented it in a spreadsheet and made the amusing gif on the right. Then I saw the joke.

The recipe

Figure 2.7. Several vectors, ##A,B,C,D,E##, and corresponding 1-forms ##\widetilde{A},\widetilde{B},\widetilde{C},\widetilde{D},\widetilde{E}##. The process of drawing ##\widetilde{U}## corresponding to a given vector ##U## is quite simple. 1) Orient the surfaces of ##\widetilde{U}## orthogonal to the vector ##U## . (Why? Because any vector ##V## that is perpendicular to ##U## must pierce no surfaces of ##\widetilde{U}## (##0=U\bullet V=U,V##) and must therefore lie in a surface of ##\widetilde{U}##.) 2) Space the surfaces of  ##\widetilde{U}## so the number of surfaces pierced by some arbitrary vector ##Y## (e.g., ##Y=U##) is equal to ##Y\bullet U##.

Note that in the figure the surfaces of ##\widetilde{B}## are, indeed, orthogonal to ##B##; those of ##\widetilde{C}## are, indeed, orthogonal to ##C##, etc. If they do not look so, that is because the reader is attributing Euclidean geometry, not Lorentz geometry, to the spacetime diagram. He should recall, for example, that because ##C## is a null vector, it is orthogonal to itself (##C\bullet C=0##), so it must itself lie in a surface of the 1-form  ##\widetilde{C}##. Confused readers may review spacetime diagrams in a more elementary text, e.g., Taylor and Wheeler (1966)."

Read it here, including punchline: 2.5 Differential forms.pdf. (6 pages)