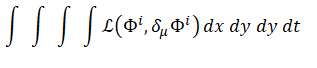Commentary 2.3 Vector as differential operator

I wanted to investigate the quite surprising point of view that a vector can be represented as a differential operator. This is the subject of section 2.3 Vectors again. At the bottom of page 66, it says

"Since a vector at a point can be thought of as a directional derivative operator along a path through that point, it should be clear that a vector field defines a map from smooth functions to smooth functions all over the manifold, by taking a derivative at each point." In the next sentence he talks of a vector field Y having an action on a function f(x^μ). e.g. Y(f) in equation (2.20).

First of all I watched some Khan Academy videos on vector fields. It was good reminder.

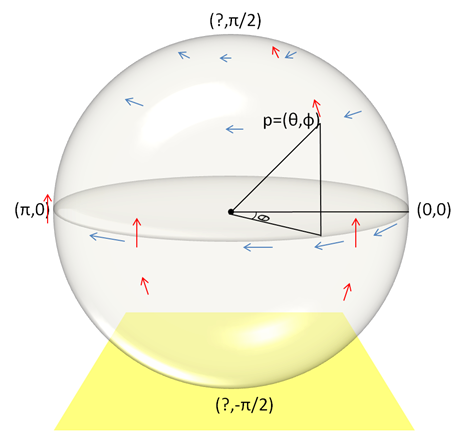
Then I imagined a sphere containing two vector fields X and Y. X is shown in blue and circles along lines of latitude decreasing as the latitude reaches the poles. Y is shown in red and always goes from south to north, also decreasing nearer the poles. I also combined them to make a vector field

Z = X + Y / 2

which would swirl upwards.

Read more at Commentary 2.3 Vector as differential operator.pdf

Commentary 2.2 Chain rule in multiple dimensions

The good old chain rule can be written as 

On page 62 we have R^m with coordinates x^a, Rⁿ with coordinates y^b and R^l with coordinates z^c. And functions f^b which maps x^a onto y^b and g^c which maps y^b  onto z^c as shown below.

Picture copied from book. Thanks.

At equation (2.12) Carroll states that the chain rule relates the partial derivative of a composition to the partial derivatives of its individual maps, so:

I'm not quite sure where the c index should go, but the left hand side is the same as 

so (2.12) looks like (2) apart from the summation over b. I was a bit surprised by this and wondered about the summation.

In fact the right hand side of (2.12) is a chain rule generalised for functions of multiple variables. I eventually found it discussed on Wikipedia under the Chain rule - Higher dimensions. By a horrible change of variables I could show that Carroll and Wikipedia were talking the same language.

On the way I thoroughly refreshed my mind on differentiation of polynomials, showing that a sample set of polynomials could be differentiated by the chain rule or by simple expansion - giving the same result. Read here if you like.

Commentary 2.2 Sphere manifold

In section 2.2 on "What is a manifold?" after equation (2.9) Sean Carroll says check the equation for yourself. The equation is

ϕ₁ is the stereographic mapping from coordinates on a sphere to the 'southern plane' as shown below. (Similar to Carroll's Figure 2.16)

The diagram shows a section through the sphere which has radius 1. The section is in the plane of (y¹, y²) and the X³ axis, so it looks oval.  The point (x¹, x², x³) on the sphere is projected onto (y¹, y²) on the southern plane which is at x³=-1. We then drop a perpendicular (dashed line) from (x¹, x², x³) onto the southern plane to (x¹, x²)  and from there to the Y¹ axis. It hits at (x¹, 0). We also drop a perpendicular from  (y¹, y²) to the Y¹ axis, it hits at (y¹, 0). From there we draw a line back up to the North Pole and draw a line straight up from (x¹, 0) to intersect it. The intersection point is inside the sphere. We now have two right angled, similar triangles in Y¹X³ plane. These give us the equation below. The left hand side is from  the sides of the larger triangle......

Read more at Commentary 2.2 sphere manifold.pdf with additional material working up to the 'Northern plane'

This was my first attempt at a 3-D diagram. They improve!

Commentary 2.2 ф(x)=|x^3| is a C^2 function

In section 2.2 on "What is a manifold?" under equation (2.8) he says ф(x)=|x³| is a C² function because it is infinitely differentiable everywhere except at x=0 where it is differentiable twice but not three times.

I had to think about that one and had a quick look at this video on the Khan academy to refresh my memory. I then got to use my own graph paper to test the assertion for myself. What fun! Now I have put it in Excel. Here is the result.

ф(x)=|x³| is in blue. It's gradient is obviously negative for x<0 and positive for x>0.

So

For x<0, ф'=-3x² and for x>=0 ф'=3x². The gradient of ф' is always positive.

So ф''=|6x|. We can now see the problem at x=0 in green.

It is hardly necessary to plot ф''' which is -6 for x<0, 6 for x>0, but undefined at x=0.

Resources

Commentary2.2.pdf

Commentary2.2.xlsx

Commentary 2.1 Red Shift

In section 2.1 on gravitational red shift he says, in the accelerating rockets:

and on the tower in a gravity field

Those are both straight forward.

He then reminds us of the Newtonian potential and that a_g = ∇Φ.

He then gets

(2.7a) comes straight from (2.5) by integrating the acceleration over time to get Δv.
But I don't see why (2.7b) follows from (2.7a).

However from (2.6) we can get

I don't follow Carroll's logic but I can get the same answer!

Resources.
The above is also in Commentary 2.1 Red Shift.pdf

Question for Physics Forums: Help with integration conventions

I am reading Spacetime and Geometry by Sean Carroll. In section 1.10 on classical field theory, he uses this formula (1.132)

The curly L is a Lagrange density. S is an action, Φ is a vector potential.

Could the integral also be written as follows?

Posted on physics forums.