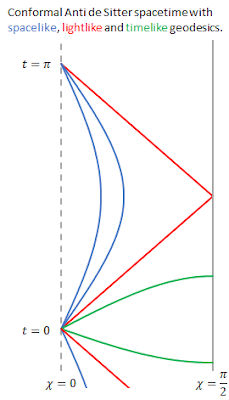
In section 8.1 we meet maximally symmetric universes. That's universes where every point in spacetime is the same. I think the only ones are de Sitter, Minkowski and Anti de Sitter. We've done flat, boring Minkowski. De Sitter and Anti de Sitter are more interesting and we do conformal diagrams for both of them. At the end of the section Carroll does conformal anti de Sitter and casually draws some geodesics on it without saying how he plotted them. I was able to put my newly learnt skills to good use and show the same curves as he did😀. My version is on the left.
He also jumps back to section 3.1 and uses the equation there for the Riemann tensor. It is$$
R_{\rho\sigma\mu\nu}=\kappa\left(g_{\rho\mu}g_{\sigma\nu}-g_{\rho\nu}g_{\sigma\mu}\right)
$$where ##\kappa## is a constant. That equation easily becomes$$
R_{\ \ \ \sigma\mu\nu}^\rho=\kappa\left(\delta_\mu^\rho g_{\sigma\nu}-\delta_\nu^\rho g_{\sigma\mu}\right)
$$so it looks like there's a really way to calculate the fiendish Riemann tensor for these special cases. Unfortunately $$
\kappa=\frac{R}{n\left(n-1\right)}
$$where ##n## is the number of dimensions and ##R## is the curvature scalar (aka Ricci scalar) which is constant in a maximally symmetric universe. Nevertheless to calculate it you have to calculate the Riemann tensor first! B*gger.
R_{\rho\sigma\mu\nu}=\kappa\left(g_{\rho\mu}g_{\sigma\nu}-g_{\rho\nu}g_{\sigma\mu}\right)
$$where ##\kappa## is a constant. That equation easily becomes$$
R_{\ \ \ \sigma\mu\nu}^\rho=\kappa\left(\delta_\mu^\rho g_{\sigma\nu}-\delta_\nu^\rho g_{\sigma\mu}\right)
$$so it looks like there's a really way to calculate the fiendish Riemann tensor for these special cases. Unfortunately $$
\kappa=\frac{R}{n\left(n-1\right)}
$$where ##n## is the number of dimensions and ##R## is the curvature scalar (aka Ricci scalar) which is constant in a maximally symmetric universe. Nevertheless to calculate it you have to calculate the Riemann tensor first! B*gger.
I still wanted to check that it was all true. We already did it for a the surface of a unit sphere, S², and have found it was constant at 2 and its Riemann tensor does satisfy the formula above. So S² is maximally symmetric. All points on the surface of a sphere are equal. The metric for conformal anti de Sitter is$$
{ds}^2=\frac{\alpha^2}{\cos^2{\chi}}\left(-{dt^\prime}^2+{d\chi}^2+\sin^2{\chi}{d\Omega_2}^2\right)
$$where ##\alpha## is some constant. So its Riemann tensor is trickier!
{ds}^2=\frac{\alpha^2}{\cos^2{\chi}}\left(-{dt^\prime}^2+{d\chi}^2+\sin^2{\chi}{d\Omega_2}^2\right)
$$where ##\alpha## is some constant. So its Riemann tensor is trickier!
As I had already calculated the Christoffel symbols for that to make the diagram above, I calculated its Riemann tensor and then its curvature scalar which is ##-12\alpha^{-2}##. So it is constant and satisfies the formula as I checked with a cunning spreadsheet.
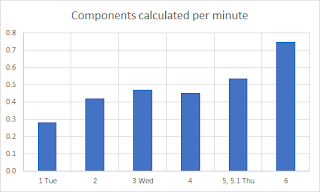
Calculating that Riemann tensor, which is a relatively easy one, took 9 hours 45 minutes over three days and six sittings. I got faster as I went along, notwithstanding long lunches preceded by a refreshing dry martini.
Read all about it at
and