In section 2.6 we met a special case of the Robertson-Walker metric for an expanding Universe. Exciting! The section was a 'playground' for our previous work. From the metric we got to
0 < q < 1. Even I could integrate that equation, but Carroll produced
by changing the variables around. As you really want how x changes as t progresses, the obvious equation
is much more informative and useful. x0 is a constant of integration, in fact where our test photon starts.
I could then get some graphs and understand what he was talking about. t must be positive. (One can't take a fractional power of a negative number.)
x0 is the point on the X axis where the light cone starts. The red x(xo) lines are the solutions for x0 = -7 the one on the left (paler) being the negative part. The x(x1) lines are for x0 = 7. The light cones always and only intersect at some t > 0 midway between their start points. There are no solutions for t < 0.
If we set q = 0 then we get our flat Minkowski space and we can have t < 0. The diagram becomes
The light cones intersect in the past (bottom open triangle) as well as in the future (top open triangle).
In the spirit of the playground, it is amusing to show the first diagram again with (impossible) t < 0. Excel does a great job!
by changing the variables around. As you really want how x changes as t progresses, the obvious equation
is much more informative and useful. x0 is a constant of integration, in fact where our test photon starts.
I could then get some graphs and understand what he was talking about. t must be positive. (One can't take a fractional power of a negative number.)
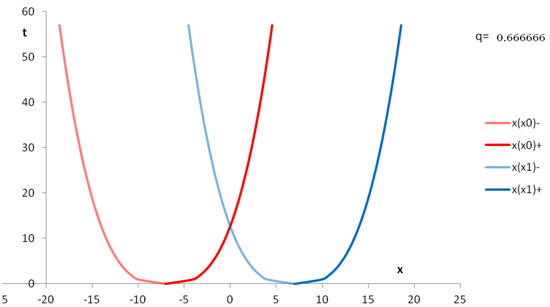 |
| Two light cones |
If we set q = 0 then we get our flat Minkowski space and we can have t < 0. The diagram becomes
 |
| Light cones in Minkowski spacetime |
The light cones intersect in the past (bottom open triangle) as well as in the future (top open triangle).
In the spirit of the playground, it is amusing to show the first diagram again with (impossible) t < 0. Excel does a great job!
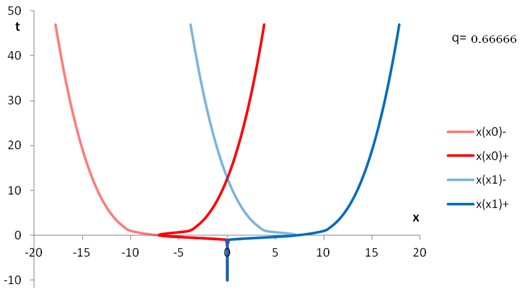 |
| Big Bang |
Read in more detail at Commentary 2.6 Expanding Universe.pdf. Includes link to spreadsheet.